Gianni Bellocchi
Gianni Bellocchi (born July 22, 1969) is a researcher in agricultural and related sciences. He is credited with the development of approaches and tools in validation of estimates and measurements. Introduction of fuzzy logic in the context of validation is often considered to be the most significant contribution to the field of model and method validation (Agronomy Journal, volume 94, pages 1222-1233 [1]; Food Analytical Methods, volume 2, pages 126-135 [2]).
He also helped spark the validation issues in agro-ecological modelling and analytical methods through his reviews of specialistic literature. His approach to the aggregation of multiple validation metrics has influenced the way validation results are viewed. In this respect he is credited with the establishment of hierarchy of preferences in validation and classification of models and methods in terms of aggregated, weighted metrics.
In the Roman Catholic Church, he is close to Communion and Liberation, the lay ecclesial movement founded by Monsignor Luigi Giussani.
Contents |
Biography
Gianni Bellocchi was born in Acquapendente and spent formative years in San Lorenzo Nuovo, in province of Viterbo (Italy), near Lago di Bolsena. His parents, Giuseppe (born 1944) and Adriana (born 1946), are retired farmers. He attended at primary and middle schools in his village, and at agricultural high school in Bagnoregio. Starting in 1988, he studied agricultural sciences at the University of Pisa and at the Sant'Anna School of Advanced Studies of Pisa. He graduated in 1993 and got a PhD in 1997. He learned statistical data processing and modelling approaches from entomologist Fabio Quaglia, physicist Franco Martorana[3], and modellers Frits W.T. Penning de Vries [4] (Wageningen University, The Netherlands) and Claudio O. Stockle[5] (Washington State University, Pullman, Washington, U.S.). Gianni joined the staff of agronomy and agro-meteorology modelers of the Research Institute for Industrial Crops[6] of Bologna in 1999, and developed a large number of scientific contributions under the leaderhsip of Marcello Donatelli[7]. In 2006-2009 he was appointed contractual agent at European Commission - Joint Research Centre of Ispra, Italy. In 2010, he became senior scientist at French National Institute for Agricultural Research (INRA), Grassland Ecosystem Research Unit (UREP). In 2011, January 25, he got the Habilitation à Diriger des Recherches from Blaise Pascal University of Clermont-Ferrand (France). He joined as member of the Italian Society for Agronomy[8], the European Society for Agronomy[9], the American Society of Agronomy[10], and the International Environmental Modelling and Software Society[11]. He is also affiliated to the Monte Pino Met European Research Observatory[12].
Model and method validation
Bellocchi's work in validation has had implications for model and analytical method assessment. Genuine insights in model results, as well as results from an analytical method, imply concomitant understandings of multiple aspects of quality assessment to be taken into account and formalized. The fuzzy set theory formalized by Professor Lofti Zadeh at the University of California in 1965 was pointed out as having a direct use to assess numerical outcomes for its ability to aggregate multiple, possibly contradictory, evaluation measures. Many of the more basic principles of this theory are now generally accepted in many areas. Its application in a context of validation opened up to a new way to investigate results from a modelling process or an analytical method. In 2001, Bellocchi and co-workers firstly introduced the possibility to use fuzzy logic to evaluate model estimates at the Second International Symposium on Modelling Cropping Systems [13] (Florence, Italy), and in 2002 the same approach was internationally acknowledged (Agronomy Journal, volume 94, pages 1222-1233). Further extensions and applications followed (as reported in Authorship).
Fuzzy logic
Multiple-metric aggregation
The procedure based on the multi-valued fuzzy set introduced by Professor Lofti Zadeh, follows the Sugeno method of fuzzy inference (Information Sciences, volume 36, pages 59–83 [14]). Three membership classes are basically defined for all metrics used in the validation work, according to an expert judgment, i.e. Favorable (F), Unfavorable (U), and partial (or fuzzy) membership, using S-shaped curves as transition possibilities in the range F to U:
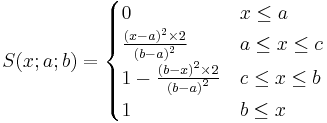
where: x = the value of the basic input; a = the lower bound of the transition interval [min(F, U)]; b = the upper bound of the transition interval [max(F, U)]; c = (a + b) /2. According to the equation, if a = F, then x ≤ a means x = F, and S(x;a;b) gives the degree of membership of the index value x to the set U. Its complement, 1 - S(x;a;b), gives the degree of membership of the index value x to the set F.
A two-stage design of a fuzzy-based rules’ inferring system is applied where firstly inputs with similar characteristics are aggregated into modules and then, using the same procedure, the modules can be aggregated into a second level integrated index called indicator. Both modules and indicator range from 0 to 1.
The control rules for estimating module values are based on logic relationships between inputs and outputs, expressed in linguistic terms by ‘if-then’ statements. For example, when two input variables (validation metrics) are aggregated four rules are required, formalized as:
____PREMISE____CONCLUSION
if x1 is F and x2 is F then yi is B1
if x1 is F and x2 is U then y2 is B2
if x1 is U and x2 is F then y3 is B3
if x1 is U and x2 is U then y4 is B4
where xi is an input variable, yi is an output variable and Bi is a conclusion (or expert weight). The value of each conjunction (… and …) is the minimum of the quantified fuzzy groups, which are obtained from complementary S-shaped distribution curves.
The output fuzzy sets for all the rules are then aggregated into a single fuzzy set. This group encompasses a range of output values, and is de-fuzzified in order to resolve a single crisp output value from the group (i.e. a value between 0 and 1). This approach uses the centroid method to obtain the representative non-fuzzy value for the output, as commonly adopted in the Sugeno-type systems. The expert reasoning runs as follows: if all input variables are F, the value of the module is 0 (good response according to all metrics used); if all indices are U, the value of the module is 1 (bad response according to all inputs used), while all the other combinations assume intermediate values. Limits F and U may come from experience, may be extracted from literature, or may be set by law. The weights can be chosen based on the analyst own experience in handling each input.
Authorship (selected)
See a full bibliography on Bellocchi's web site [15].
Fuzzy logic and validation
- Alexandrov G.A., Ames G., Bellocchi G., Bruen M., Crout N., Erechtchoukova M., Hildebrandt A., Hoffman F., Jackisch C., Khaiter P., Mannina G., Matsunaga T., Purucker S.T., Rivington M., Samaniego L., 2011. Technical assessment and evaluation of environmental models and software: Letter to the Editor. Environmental Modelling and Software, 26, 328-336. [16]
- Bellocchi G., De Giacomo M., Fori N., Mazzara M., Palmaccio E., Savini C., Di Domenicantonio C., Onori R., van den Eede G., 2010. Testing the interaction between analytical modules: an examples with Roundup Ready® soybean line GTS 40-3-2. BMC Biotechnology, 10:55 doi:10.1186/1472-6750-10-55. [17]
- Bellocchi G., Bertholet V., Hamels S., Moens W., Remacle J., van den Eede G., 2010. Fuzzy-logic based strategy for validation of multiplex methods: example with qualitative GMO assays. Transgenic Research, 19, 57-65. [18]
- Bellocchi G., Rivington M., Donatelli M., Matthews K.B., 2010. Validation of biophysical models: issues and methodologies. A review. Agron. Sustain. Dev., 30, 109-130. [19]
- Bellocchi G., Savini C., van den Bulcke M., Mazzara M., van den Eede G., 2010. Fuzzy-logic based procedures for GMO analysis. Accreditation and Quality Assurance, 15, 637-641. [20]
- Foscarini F., Bellocchi G., Confalonieri R., Savini C., van den Eede G., 2010. Sensitivity analysis in fuzzy systems: integration of SimLab and DANA. Environmental Modelling & Software, 25, 1256-1260. [21]
- Lievens A., Bellocchi G., De Bernardi D., Savini C., Mazzara M., Moens W., van den Bulcke M., van den Eede G., 2010. Use of pJANUSTM-02-001 as calibrator plasmid for GTS 40-3-2 (Roundup Ready Soybean) detection: an inter-laboratory trial assessment. Analytical and Bioanalytical Chemistry, 396, 2165-2173. [22]
- Confalonieri R., Acutis M., Bellocchi G., Donatelli M., 2009. Multi-metric evaluation of the models WARM, CropSyst, and WOFOST for rice. Ecological Modelling, 220, 1395-1410. [23]
- Confalonieri R., Bellocchi G., Boschetti M., Acutis M., 2009. Evaluation of parameterization strategies for rice modelling. Spanish Journal of Agricultural Research, 7, 680-686. [24]
- Bellocchi G., Acutis M., Paoletti C., Confalonieri R., Trevisiol P., Grazioli E., Delobel C., Savini C., Mazzara M., van den Eede G., 2008. Expanding horizons in the validation of GMO analytical methods: fuzzy-based expert systems. Food Analytical Methods, 2, 126-135. [25]
- Bellocchi G., Donatelli M., Acutis M., Habyarimana E., 2008. A software component for model output evaluation. iEMSs 2008 International Congress on Environmental Modelling and Software: "Integrating sciences and information technology for environmental assessment and decision making". International Environmental Modelling and Software Society, 7–10 July, Barcelona, Spain, 2, 1063-1069. [26]
- Bellocchi G., Foscarini F., Canonico M., van den Eede G., 2008. DANA: a platform-independent component for data analysis and assessment. 1st Global Conference on GMO Analysis, 24–27 June, Villa Erba, Como, Italy, 40. [27]
- Bellocchi G., Foscarini F., Canonico M., van den Eede G., 2008. Web components for development of computational methods: example with fuzzy logic rules. iEMSs 2008 International Congress on Environmental Modelling and Software: "Integrating sciences and information technology for environmental assessment and decision making". International Environmental Modelling and Software Society, 7–10 July, Barcelona, Spain, 2, 1077-1085. [28]
- Leimanis S., Hamels S., Nazé F., Mbongolo Mbella G., Sneyers M., Hochegger R., Broll H., Roth L., Dallmann K., Micsinai A., La Paz J.L., Pla M., Brünen-Nieweler C., Papazova N., Taverniers I., Hess N., Kirschneit B., Bertheau Y., Audeon C., Laval V., Busch U., Pecoraro S., Neumann K., Rösel S., van Dijk J., Kok E., Bellocchi G., Foti N., Mazzara M., Moens W., Remacle J., van Den Eede G., 2008. Validation of a GMO multiplex screening assay by the use of microarray. Eur. Food Res. Technol., 227, 1621-1632. [29].
- Acutis M., Trevisiol P., Confalonieri R., Bellocchi G., Grazioli E., Van Den Eede G., Paoletti C., 2007. Analytical method performance evaluation (AMPE) - A software tool for analytical method validation. Journal of AOAC International, 90, 1432-1438. [30]
- Bellocchi G., 2007. Using fuzzy logic to develop a system to test solar radiation models. In: Smith J., Smith P. (eds.) Introduction to environmental modelling - Chapter 3: How to evaluate a model. Oxford University Press, Oxford, United Kingdom, web link from the book at http://www.oup.com/uk/orc/bin/9780199272068/01student/weblinks/ch03/box3a.pdf.
- Criscuolo L., Donatelli M., Bellocchi G., Acutis M., 2007. A component and a software application for model output evaluation. Farming Systems Design 2007, an international symposium on Methodologies for Integrated Analysis of Farm Production Systems, 10–12 September, Catania, Italy, 2, 211-212. [31]
- Diodato N., Bellocchi G., 2007. Modelling solar radiation over complex terrains using monthly climatological data. Agricultural and Forest Meteorology, 144, 111-126. [32]
- Diodato N., Bellocchi G., 2007. Modelling reference evapotranspiration over complex terrains from minimum climatological data. Water Resources Research, 43, doi:10.1029/2006WR005405. [33]
- Hamels S., Leimanis S., Mazzara M., Bellocchi G., Foti N., Moens W., Remacle J., van Den Eede G., 2007. Microarray method for the screening of EU approved GMOs by identification of their genetic elements. Report of validation coordinated by the Community Reference Laboratory for GM Food and Feed of the Joint Research Centre, Institute for Health and Consumer Protection, Biotechnology and GMOs Unit, Ispra, Italy. [34]
- Bellocchi G., Grazioli E., Acutis M., Confalonieri R., Paoletti C., Trevisiol P., 2006. Application of software AMPE to evaluate the performance of GM grains detection methods. 9th European Society for Agronomy Congress, 4–7 September, Warsaw, Poland, 743-744. [35]
- Fila G., Donatelli M., Bellocchi G., 2006. PTFIndicator: an IRENE_DLL-based application to evaluate estimates from pedotransfer functions by integrated indices. Environmental Modelling and Software, 21, 107-110. [36]
- Rivington M., Bellocchi G., Matthews K.B., Buchan K., 2005. A detailed evaluation of methods to estimate solar radiation data for use in simulation models and experimental analysis. Agricultural and Forest Meteorology, 135, 228-243. [37]
- Bellocchi G., 2004. Appendix A: Numerical indices and test statistics for model evaluation. In Pachepsky Y., Rawls W. (eds.) Development of pedotransfer functions in soil hydrology. Elsevier, Amsterdam, The Netherlands, 394-400. [38]
- Bellocchi G., Smith J., Donatelli M., Smith P., 2004. Improvements in time mismatch analysis of model estimates. 8th European Society for Agronomy Congress, 11–15 July, Copenhagen, Denmark, 221-222. [39]
- Donatelli M., Wösten J.H.M., Bellocchi G., 2004. Evaluation of pedotransfer functions. In Pachepsky Y., Rawls W. (eds.) Development of pedotransfer functions in soil hydrology. Elsevier, Amsterdam, The Netherlands, 400-405. [40]
- Fila G., Bellocchi G., 2004. Appendix B: Fuzzy expert systems. In Pachepsky Y., Rawls W. (eds.) Development of pedotransfer functions in soil hydrology. Elsevier, Amsterdam, The Netherlands, 357-363. [41]
- Fila G., Donatelli M., Bellocchi G., 2004. An IRENE_DLL application to evaluate estimates from pedotrasnfer functions by integrated indices. 8th European Society for Agronomy Congress, 11–15 July, Copenhagen, Denmark, 253-254. [42]
- Fila G., Bellocchi G., Acutis M., Donatelli M., 2003. IRENE: a software to evaluate model performance. European Journal of Agronomy, 18, 369-372. [43]
- Fila G., Bellocchi G., Donatelli M., Acutis M., 2003. IRENE_DLL: A class library for evaluating numerical estimates. Agronomy Journal, 95, 1330-1333. [44]
- Bellocchi G., Acutis M., Fila G., Donatelli M., 2002. An indicator of solar radiation model performance based on a fuzzy expert system. Agronomy Journal, 94, 1222-1233. [45]
- Fila G., Bellocchi G., Donatelli M., Acutis M., 2001. IRENE: a software to test model performance. 2nd International Symposium on Modelling Cropping Systems, 16–18 July, Florence, Italy, 215-216. [46]
- Bellocchi G., Acutis M., Donatelli M., Fila G., 2001. An indicator of solar radiation model performance based on fuzzy rules. 2nd International Symposium on Modelling Cropping Systems, 16–18 July, Florence, Italy, 49-50. [47]